Chapitre 5 : Les vecteurs

I] Définitions

Définition : Un vecteur est défini par trois composantes :

• Sa direction : celle de la droite qui porte le vecteur
• Son sens : oriente le vecteur (par la flèche) ex : sens de A vers B
• Sa longueur (norme en physique) : il suffit de mesurer.

Remarque : De ce fait, un vecteur peut être déplacé n'importe où dans le plan, à condition que ses trois composantes, direction, sens et longueur ne changent pas.

Propriétés :

• Deux vecteurs sont égaux si et seulement si ils ont même direction, même sens et même longueur.
• Si alors, ABDC est un parallélogramme.

II] Opérations sur les vecteurs

Somme: Soit et deux vecteurs, alors qui est la diagonale issue du paralleloogramme formé par les vecteurs et (cf. dessin).

Remarque : Pour (les deux vecteurs issus d'un même point), on utilise la même méthode.

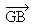
Relation de Chasles : Pour tous points A, B, C, on a : . En pratique, (à ne pas mettre sur une copie ) le point à droite du 1^er vecteur doit être le même que le point à gauche du 2^nd vecteur.

Vecteurs opposés : Soit un vecteur, on note le vecteur opposé à . En pratique, est de sens contraire à

Remarques :

• vecteur nul. (d'après Chasles)
• Soustraire 2 vecteurs correspond à additionner l'un avec l'opposé du 2^nd

III] Colinéarité, Multiplication par un réel.

Définition : Soit un vecteur et k un réel. Le vecteur résultant de la multiplication de k par est :

• Si k=0,
• Si k>0, et ont même sens, même direction mais de longueurs différentes.
• Si k<0, et ont même direction, mais sont de sens opposés et n'ont pas même longueur.

Propriétés :

Colinéarité : Deux vecteurs et sont colinéaires si et seulement si :

• L'un des vecteurs est nul
• Il existe un réel k tel que

Propriétés :

• 3 points A, B, C sont alignés si et seulement si et sont colinéaires.
• Si 2 droites (AB) et (CD) sont parallèles, alors et sont colinéaires.
• Inversement, si et sont colinéaires, alors les droites (AB) et (CD) sont parallèles ou confondues.

IV] Autres Propriétés utiles

Milieu d'un segment : Si I milieu de [AB], alors

Centre de Gravité d'un triangle : Soit G, le centre de gravité d'un triangle ABC, alors :

Conseil : N'oubliez jamais CHASLES, il est à utiliser au moins une fois (sinon plus) dans tous les problèmes conséquents sur les vecteurs (et pas seulement en seconde), en effet la relation est utile pour insérer un point dans un vecteur ou simplifier un expression.