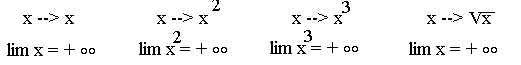
Chapitre 6 : Les Limites

I) Limite en infinie, en + _°°

Chacune des fonctions suivantes tend vers + _°° lorsque x tend vers + _°°

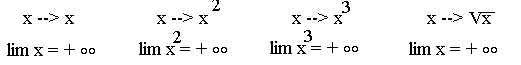
II) Limite finie en + _°°

Chacune des fonctions tend vers 0 quand x tend vers

Définition : dire que f(x) = 2, cela signifie que limite [ f(x) -2 ] = 0

III) Notion d'asymptote horizontale

• M a pour coordonnées M ( x ; f(x) )
• m a pour coordonnées m ( x ; 2 )
• mM = |f(x) -2 |

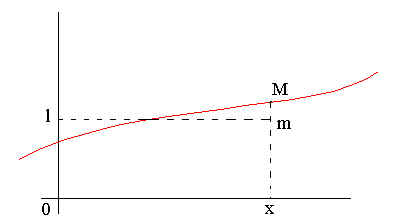
Définition : lorsque lim f(x) =2 (quand x --> + _°° ), la distance mM tend vers 0

On dit alors que la droite d'équation y = l est une asymptote à la courbe

IV) limite en a ( a réel )

La fonction f étant définie sur un intervalle, ou une réunion d'intervalle, nous envisagerons les limites lorsquef est définie en a, oubien lorsque a est une borne de l'intervalle de définition de F.

Exemple: * f(x) = x² +1, f est définie en 0 => lim f(x) = 1 (quand x tend vers 0)

1) Chacune des fonctions suivantes tend vers 0 lorsque x tend vers 0

• x --> x
• x --> x²
• x --> V(x)

2) Des situations de base

Le changement de variable x = a + b permet de ramener la recherche de limite en a, à celle de 0

Dire lim f(x) = l (lorsque x --> a) signifie aussi lim f(a+b)= l (lorsque l --> 0)

3) Fonction définie en a

Si f est définie en a et si f admet une limite en a alors lim f(x) = f(a) (lorsque x-->a)

V) Limite infinie, Asymptote vertical

Définition : lorsque la fonction f admet une limite infinie en a, on dit alors que la droite d'équation x = a est une asymptote verticale à la courbe

Exemple : f(x) = 1/x , lim f(x)= + _°° (lorsque x -->0)